贝尔曼福特算法——负权值单源最短路径
贝尔曼福特算法——负权值单源最短路径
问题:具有负权值非环图的单源最短路径算法
git地址:https://github.com/944613709/HIT-Data-Structures-and-Algorithms
算法思想:
对图中的边进行V-1轮遍历,对所有的边松弛(对每条边v1->v2,如果d[v2]+Weight(v1->v2)<d[v2]就更新d[v2]),利用上述遍历松弛可以得到最终最短路径,和再次松弛判断有无负权值环(遍历都结束后,若再进行一次遍历,还能得到到某些节点更短的路径的话,则说明存在负环路)
算法步骤:
0. 建立图
1. 初始化d,如果s->v1有边,则d[v1]=G.ENode[s][v2],并且path设为s的下标,而d[s]=0;
*2.*对图进行V-1次松弛
1.1**每一次松弛,就是去遍历图的所有边,如果可以做到d[v1]+G.ENode[v1][v2] (v1->v2的weight) <d[v2],就更新d[v2]
*3.*再次进行遍历松弛,如果还能得到新的d的值,则代表存在负环路(环上权值和<0)
测试样例:
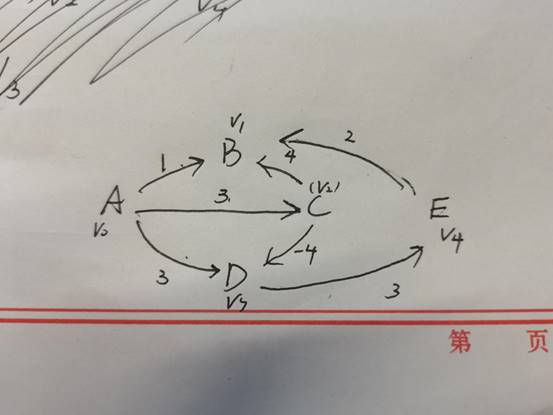
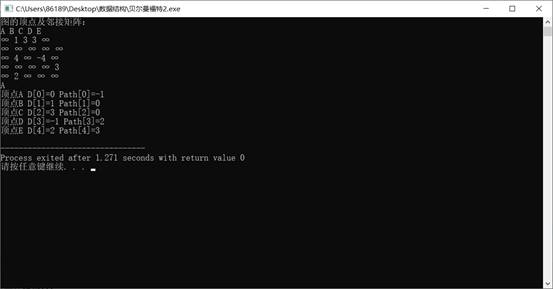
具体代码
**
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303- #include<bits/stdc++.h>**
**#define MaxVerNum 100 //****顶点最大数目值**
**#define INF 0x3f3f3f3f//****作为最大值**
**using namespace std;**
**//****图的数据结构**
**typedef struct Graph**
**{**
**char VNode[MaxVerNum];//****顶点表**
**int ENode[MaxVerNum][MaxVerNum];//****弧表**
**int numVNode, numARC;//****顶点数、弧数**
**}Graph;**
**int D[MaxVerNum]; //****到各个顶点的最短路径**
**int Path[MaxVerNum]; //****记录前驱**
**void InitGraph(Graph &G)**
**{**
**memset(G.VNode, '#', sizeof(G.VNode));//****初始化顶点表**
**//****初始化弧表**
**for (int i = 0; i < MaxVerNum; i++)**
**for (int j = 0; j < MaxVerNum; j++)**
**G.ENode[i][j] = INF;**
**G.numARC = G.numVNode = 0; //****初始化顶点数、弧数**
**}**
**bool InsertNode(Graph &G, char v)**
**{**
**if (G.numVNode < MaxVerNum)**
**{**
**G.VNode[G.numVNode++] = v;**
**return true;**
**}**
**return false;**
**}**
**bool InsertENode(Graph &G, char v, char w, int weight)**
**{**
**int p1, p2;//v,w****两点下标**
**p1 = p2 = -1;//****初始化**
**for (int i = 0; i<G.numVNode; i++)//****寻找顶点下标**
**{**
**if (G.VNode[i] == v)p1 = i;**
**if (G.VNode[i] == w)p2 = i;**
**}**
**if (-1 != p1&&-1 != p2)//****两点均可在图中找到**
**{**
**G.ENode[p1][p2] = weight;//****有向图邻接矩阵不对称**
**G.numARC++;**
**return true;**
**}**
**return false;**
**}**
**void Bellman_Ford(Graph G, int v)**
**{**
**//****初始化**
**int n = G.numVNode;//n****为图的顶点个数**
**for (int i = 0; i < n; i++)**
**{**
**D[i] = G.ENode[v][i];**
**if (D[i] < INF)Path[i] = v;**
**else Path[i] = -1;**
**}**
**D[v] = 0;**
**for(int i=0;i<G.numVNode-1;i++)**
**for(int j=0;j<G.numVNode;j++)**
**for(int k=0;k<G.numVNode;k++)**
**if (D[k] > D[j] + G.ENode[j][k])**
**{**
**D[k] = D[j] + G.ENode[j][k];**
**Path[k] = j;**
**}**
**bool flag = true;**
**for (int j = 0; j<G.numVNode - 1; j++)**
**for (int k = 0; k<G.numVNode - 1; k++)**
**if (D[k] > D[j] + G.ENode[j][k])**
**{**
**flag = false;**
**break;**
**}**
**if(flag == false)**
**{**
**cout << "****有负圈错误" << endl;**
**exit(0);**
**}**
**for(int i=0;i<n;i++)**
**{**
**cout<<"****顶点"<<G.VNode[i]<<" ";**
**cout<<"D["<<i<<"]"<<"="<<D[i]<<" ";**
**cout<<"Path["<<i<<"]="<<Path[i];**
**cout<<endl;**
**}**
**}**
**void CreateGraph(Graph &G) //****读入边和顶点建立邻接矩阵**
**{**
**FILE \*p;**
**assert((p=fopen("MatGraph.txt","r"))!=NULL);**
**int n;**
**fscanf(p,"****顶点个数=%d;",&n);**
**for(int i=0;i<n;i++)**
**{**
**char V;**
**fscanf(p,"%c;",&V);**
**if (InsertNode(G, V)) continue;//****插入点**
**else {**
**cout << "****输入错误!" << endl; break;**
**}**
**}**
**int m;**
**char flag;**
**fscanf(p,"****边个数=%d;",&m);**
**for(int i=0;i<m;i++)**
**{**
**char V1,V2;**
**int weight;**
**fscanf(p,"%c,%c,%d;",&V1,&V2,&weight);**
**if(InsertENode(G,V1,V2,weight))**
**continue;**
**}**
**fclose(p);**
**cout << "****图的顶点及邻接矩阵:" << endl;**
**for (int i = 0; i < G.numVNode; i++)**
**{**
**cout << G.VNode[i] << " ";**
**}**
**cout << endl;**
**for (int i = 0; i < G.numVNode; i++)**
**{**
**for (int j = 0; j < G.numVNode; j++)**
**{**
**if (G.ENode[i][j] == INF)cout << "∞ ";**
**else cout << G.ENode[i][j] << " ";**
**}**
**cout << endl;**
**}**
**}**
**int main()**
**{**
**Graph G;**
**InitGraph(G);**
**CreateGraph(G);**
**char V;**
**int v = -1;**
**cin >> V;**
**for (int i = 0; i < G.numVNode; i++)**
**if (G.VNode[i] == V)**
**v = i;**
**if (v == -1)**
**{**
**cout << "ERROR" << endl;**
**return 0;**
**}**
**Bellman_Ford(G,v);**
**}**
贝尔曼福特算法——负权值单源最短路径
http://yoursite.com/2023/05/16/贝尔曼福特算法——负权值单源最短路径/