双向链表实现约瑟夫问题
问题:知n个人围坐在一张圆桌周围。从编号为k的人开始报数,数到m的那个人出列;他的下一个人又从1开始报数,数到m的那个人又出列;依此规律重复下去,直到圆桌周围的人全部出列。
算法思想:
\1. 构建n个结点的双向链表,初始化按照先后顺序给链表的每个节点data值赋值为i(代表是链表第i个)
\2. 执行search函数,从Head开始寻找第P个节点,while循环head = head->next;直到来到第P个结点
\3. 执行Jump函数,将从当前head的前m-1次结点进行正常报数,然后返回第m个结点
\4. 对Jump函数返回来的第m个结点作为新head执行Delete语句,删除当前的结点,并且返回下一个节点,进行下一轮报数
\5. 利用Delete函数返回来的结点作为新head,重复3,4操作
\6. 上述重复操作总共执行n-1次出列之后,剩下最后一个人
算法步骤:
\1. 建立n个结点的双向链表
(1) 定义一个Node *head作为头结点data赋值1,再定义一个Node *tail记录尾结点
(2) For循环n-1次,for(int i=2;i<=len;i++)
① 定义Node *node,并且将data值赋值为当前的i
② 尾插法,将node插入链表
\2. 执行search函数
(1) 执行while循环直到第k个结点,while (head->data != k)
① head = head->next;
(2) 返回第k个结点Return head
\3. 利用while循环对jump和delete重复操作,同时利用count记录出列次数
3.1 执行Jump函数
(1) int count=0;利用count计数记录报数
(2) While循环直到count=m-1
① Count++代表计数加1
② Printf执行报数
③ 让head指向下一位结点
\1) 如果head此时已经指向尾结点,则while循环不断head=head->pre,直到head再次指向链表第一个节点
\2) 如果head不指向尾结点,则head=head->next;即可
(3) 返回结点Return head
3.2执行Delete语句
(4) Node *temp=head;
(5) 执行printf,声明这个节点要被删除,分三种情况讨论
① 对于删除头节点(temp->pre == NULL),直接 head=head->next;然后temp->next=NULL;head->pre=NULL;free(temp); return head;
② 对于删除尾结点if(temp->next == NULL) ,利用while循环head=head->pre;,使得head跳到链表第一个,然后执行删除原尾结点temp->pre->next=NULL;temp->pre=NULL;free(temp);
③ 对于删除中间结点head=head->next; temp->pre->next=temp->next; temp->next->pre=temp->pre; free(temp);
测试样例:
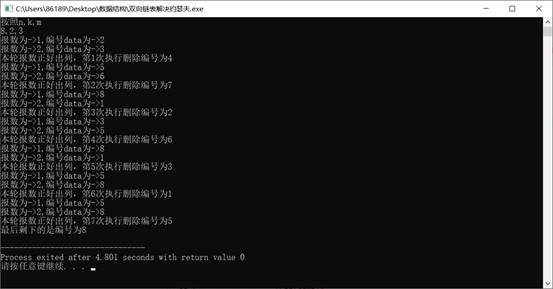
具体代码
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int delTime=0;
typedef struct Node
{
int data;
struct Node *pre;
struct Node *next;
}Node;
**Node* CreatNode(int data)//**新建结点并赋值
{
Node *node=(Node*)malloc(sizeof(Node));
node->data=data;
node->pre=NULL;
node->next=NULL;
return node;
}
Node* CreatList(int len)
{
int num=1;
Node *head= CreatNode(1);
Node *tail=head;
for(int i=2;i<=len;i++)
{
Node *node=CreatNode(i);
tail->next=node;
node->pre=tail;
tail=tail->next;
}
tail->next=NULL;
return head;
}
**Node* Delete(Node *head)//**删除当前的,并且返回下一个节点,进行下一轮报数
{
Node *temp=head;
**delTime++;//**用以判断是否到删除的数
*printf(“本轮报数正好出列,第%d次执行删除编号为%d\n”,delTime,temp->data);*
**if(temp->pre == NULL)//**对于删除头节点
{
head=head->next;
temp->next=NULL;
head->pre=NULL;
free(temp);
return head;
}
**/***判断是否是尾节点*/
**else if(temp->next == NULL)//**对于删除尾结点
{
while(head->pre!=NULL)
*head=head->pre;//删除后head跳到当前链表第一个*
temp->pre->next=NULL;
temp->pre=NULL;
free(temp);
return head;
}
**else//**删除中间结点
{
head=head->next;
temp->pre->next=temp->next;
temp->next->pre=temp->pre;
free(temp);
return head;
}
}
*Node *Search(Node *head, int k) { //从Head开始寻找第P*个节点
while (head->data != k) {
head = head->next;
}
return head;
}
*Node *Jump(Node *head, int m)//将head前m-1次正常报数,然后返回第m次*
{
int count=0;
*while(count!=m-1)//前m-1个人都能正常报数*
{
count++;
**printf(“****报数为->%d,编号data为->%d\n”,count,head->data);//**报数
if(head->next==NULL)
{
while(head->pre!=NULL)
head=head->pre;
**}//**换行
else
head=head->next;
}
return head;
}
*int main()//已知n个人围坐在一张圆桌周围。从编号为k的人开始报数,数到m的那个人出列;他的下一个人又从1开始报数,数到m*的那个人又出列;依此规律重复下去,直到圆桌周围的人全部出列。(**摘自百度百科)
{
int n,k,m;
int count=0;
**printf(“**按照n,k,m\n”);
while(scanf(“%d,%d,%d”,&n,&k,&m)!=3)
{
}
Node *head=CreatList(n);
head=Search(head,k);
*while(count!=n-1)//执行n-1次出列,来完成剩下最后一个人*
{
count++;
*head=Jump(head,m);//将head前m-1次正常报数,然后返回第m次*
**head=Delete(head);//**删除当前的,并且返回下一个节点,进行下一轮报数
}
**printf(“**最后剩下的是编号为%d\n”,head->data);
}