外部排序&&败者树&&k路归并排序

目录

内部排序和外部排序

为什么外部排序得用多路归并？

概要

[BAT 经典算法笔试题 —— 磁盘多路归并排序 - 掘金](#BAT 经典算法笔试题 —— 磁盘多路归并排序 - 掘金)

外部排序的具体过程

流程思路概述

[ 流程具体过程](# 流程具体过程)

多路归并排序的具体实现

内排序—简单二路归并参考力扣

二路归并排序的思路

外排序–k路归并排序–相关知识补充

外排序需要时间优化

优化归并过程—引入胜者树,败者树

胜者树图

败者树图

败者树的具体实现，java代码

[ 辅助数据结构Chunk与Record](# 辅助数据结构Chunk与Record)

[ 败者树LoserTree，直接运行main即可](# 败者树LoserTree，直接运行main即可)

整个外部排序的模拟实现代码

内部排序和外部排序

img点击并拖拽以移动编辑

内部排序：整个的排序过程都在内存中进行排序

外部排序：对大文件进行排序，无法将整个需要排序的文件复制到内存，所以会把文件存储到外村，等排序时再把数据一部分一部分地调入内存进行排序，整个排序继续多次内存和外存的交换。

  1. 我们的k路归并排序，既可以作为内部排序又可以外部排序，这完全取决于使用场景，反正都行
  2. 外部排序一般都采用归并排序！

为什么外部排序得用多路归并？

概要

BAT 经典算法笔试题 —— 磁盘多路归并排序 - 掘金

原文链接：https://blog.csdn.net/a574780196/article/details/122646309

​ 假定现在有一包含大量整数的文本文件存放于磁盘中，其文件大小为10GB，而本机内存只有4GB。此时若我们要对该文件中的所有整数进行升序排序，肯定不能直接将文件中的所有数据一次性读入内存中，再使用快速、归并等排序算法对这么大规模的整数进行排序。

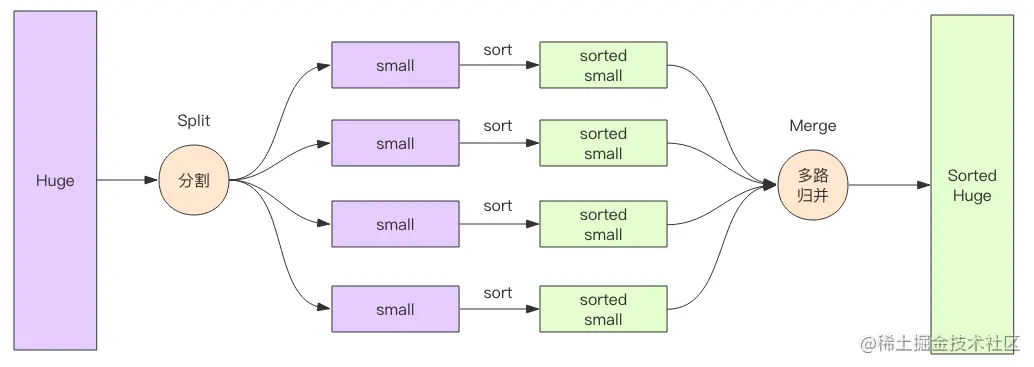
​ 好像陷入了难题？ 我们不妨换一个思路，为何不将10GB大文件拆分为10个1GB的小文件呢？ 逐个对10个文件进行排序后，再将其写入磁盘中，此时就得到了10份已排序后的临时文件。

​ 每一份文件都是一个升序序列，这时问题就转换为如何合并这10路升序序列为1路升序序列。正因为待合并的数据路数比较多，所以才有了多路归并这一说法。

简单来说就是：

链接：https://juejin.cn/post/6844903762621005837

​ 多路归并排序在大数据领域也是常用的算法，常用于海量数据排序。当数据量特别大时，这些数据无法被单个机器内存容纳，它需要被切分位多个集合分别由不同的机器进行内存排序（map 过程），然后再进行多路归并算法将来自多个不同机器的数据进行排序（reduce 过程），这是流式多路归并排序

img

点击并拖拽以移动编辑

外部排序的具体过程

参考天勤

流程思路概述

img点击并拖拽以移动编辑

img点击并拖拽以移动编辑

流程具体过程

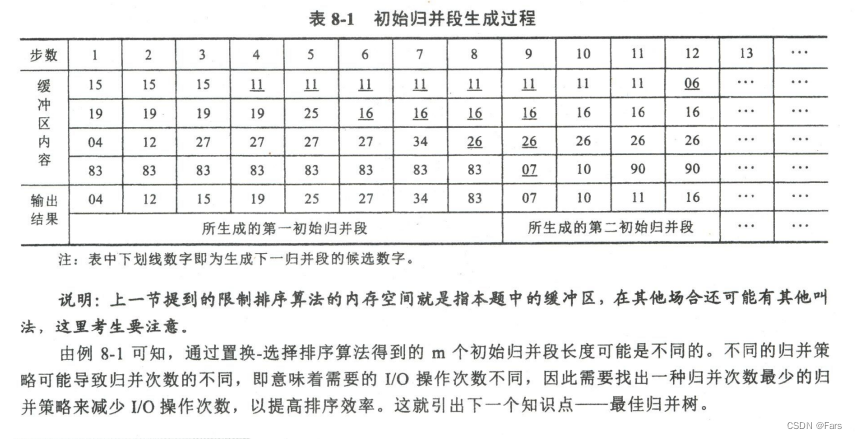
1.将外存大文件作为流输入，利用置换-选择排序算法—然后输出为多个小的已排序好的chunk（初始归并段）

​ 采用置换-选择排序算法构造初始归并段的过程;根据缓冲区大小，由外存读入记录，当记录充满缓 冲区后，选择最小的（假设升序排序）写回外存，其空缺位置由下一个读入记录来取代，输出的记录成 为当前初始归并段的一部分

img点击并拖拽以移动编辑

2.用败者树归并

  1. 通过败者树将刚才的多个chunk归并
    1. 利用败者树选择所有chunk中头部最小的元素，并把它放进外存，即ls[0]对应的bq
    2. 更换刚才被选出来的元素pop，换成它的chunk的下一个元素放在bq，调整败者树
    3. 如果某个chunk空了，则剔除该chunk，然后调整败者树
    4. 循环以上1~3直到全部chunk为空

img点击并拖拽以移动编辑

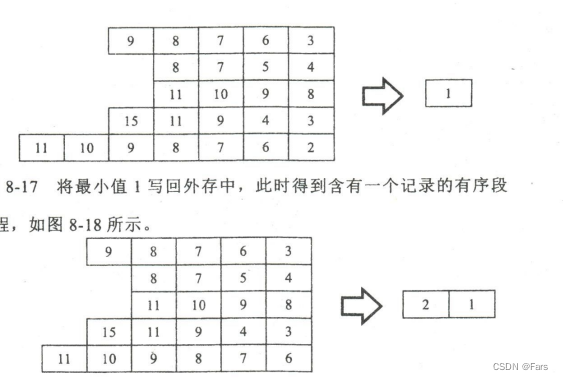
这一步对应的是下图过程

img点击并拖拽以移动编辑

多路归并排序的具体实现

内排序—简单二路归并参考力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
void mergeSort(int[] nums, int l, int r) {
    // 终止条件
    if (l >= r) return;
    // 递归划分
    int m = (l + r) / 2;
    mergeSort(nums, l, m);
    mergeSort(nums, m + 1, r);
    // 合并子数组
    int[] tmp = new int[r - l + 1]; // 暂存需合并区间元素
    for (int k = l; k <= r; k++)
        tmp[k - l] = nums[k];
    int i = 0, j = m - l + 1;       // 两指针分别指向左/右子数组的首个元素
    for (int k = l; k <= r; k++) {  // 遍历合并左/右子数组
        if (i == m - l + 1)
            nums[k] = tmp[j++];
        else if (j == r - l + 1 || tmp[i] <= tmp[j])
            nums[k] = tmp[i++];
        else {
            nums[k] = tmp[j++];
        }
    }
}

// 调用
int[] nums = { 3, 4, 1, 5, 2, 1 };
mergeSort(nums, 0, len(nums) - 1);

作者：Krahets
链接：https://leetcode.cn/circle/article/zeM9YK/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

点击并拖拽以移动

二路归并排序的思路

img点击并拖拽以移动编辑

img点击并拖拽以移动编辑

​ 内排序—–简单2路归并图

img点击并拖拽以移动编辑

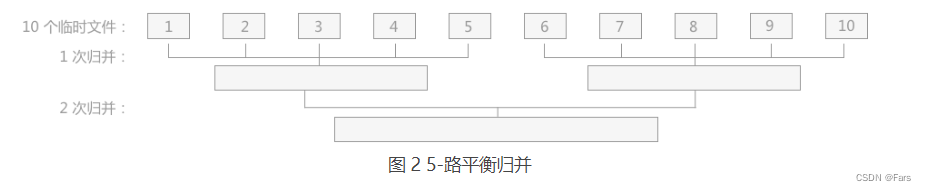
​ 内排序—–简单5路归并图

外排序–k路归并排序–相关知识补充

外排序需要时间优化

外部排序的总时间=内部排序所需的时间+外存信息读写的时间+内部归并所需的时间

显然，外存信息读写的时间远大于内部排序和内部归并的时间，因此应适当减少I/O次数

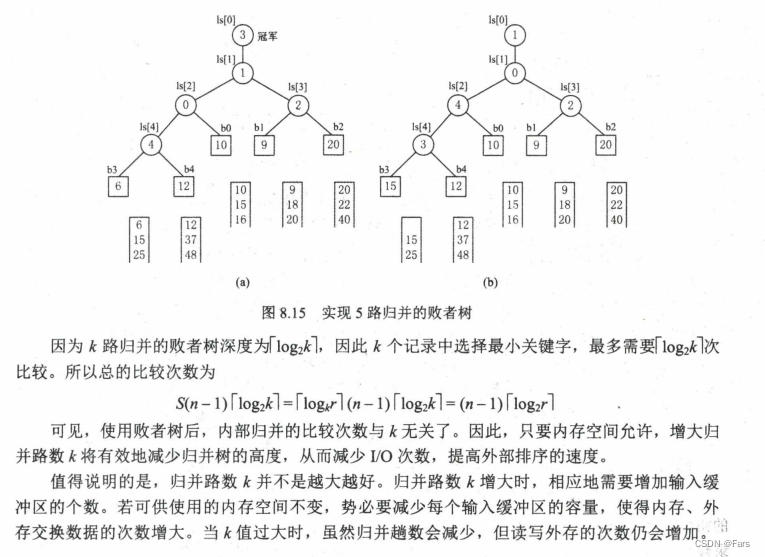
可以适当,增大归并路数，可减少归并趟数，进而减少总的磁盘I/O次数

优化归并过程—引入胜者树,败者树

不能用普通的内部归并->引入败者树

img点击并拖拽以移动编辑

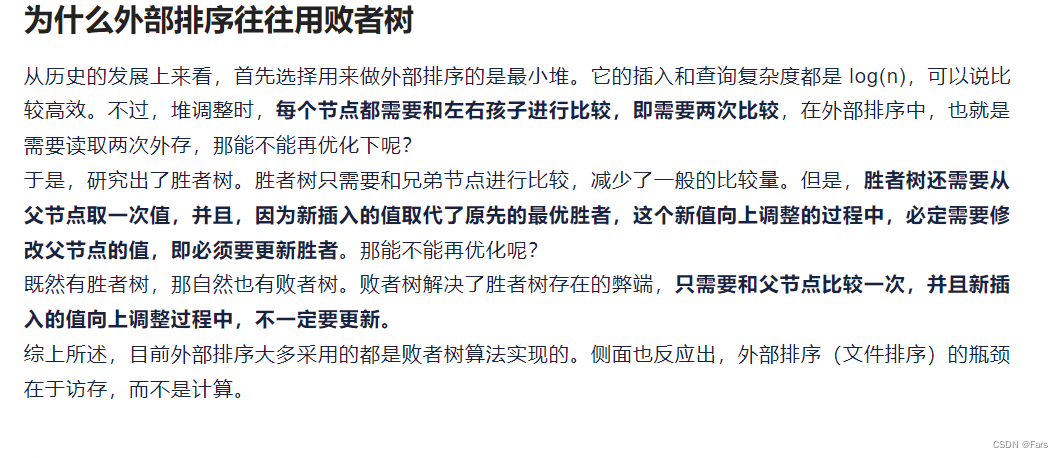
  1. 一般外部排序用的是败者树
  2. 胜者树的优点：一个选手的值改变了，可以很方便的修改当前胜者树
  3. 败者树可以说是胜者树的一个变种，是胜者树的一种优化，当一个选手的值改变了，比败者树可以很方便的修改当前胜者树
  4. 历史上：外部排序先用的最小堆，然后优化变种成了胜者树，再优化变种成了败者树

理解胜者树和败者树的关键：

胜者树和败者树都是拿赢家去比下一轮，但是不同的是，胜者树的中间结点记录的是胜者的标号；而败者树的中间结点记录的败者的标号。（败者树虽然记录的是败者标号，但是也依然会把胜者传给下一轮去比）

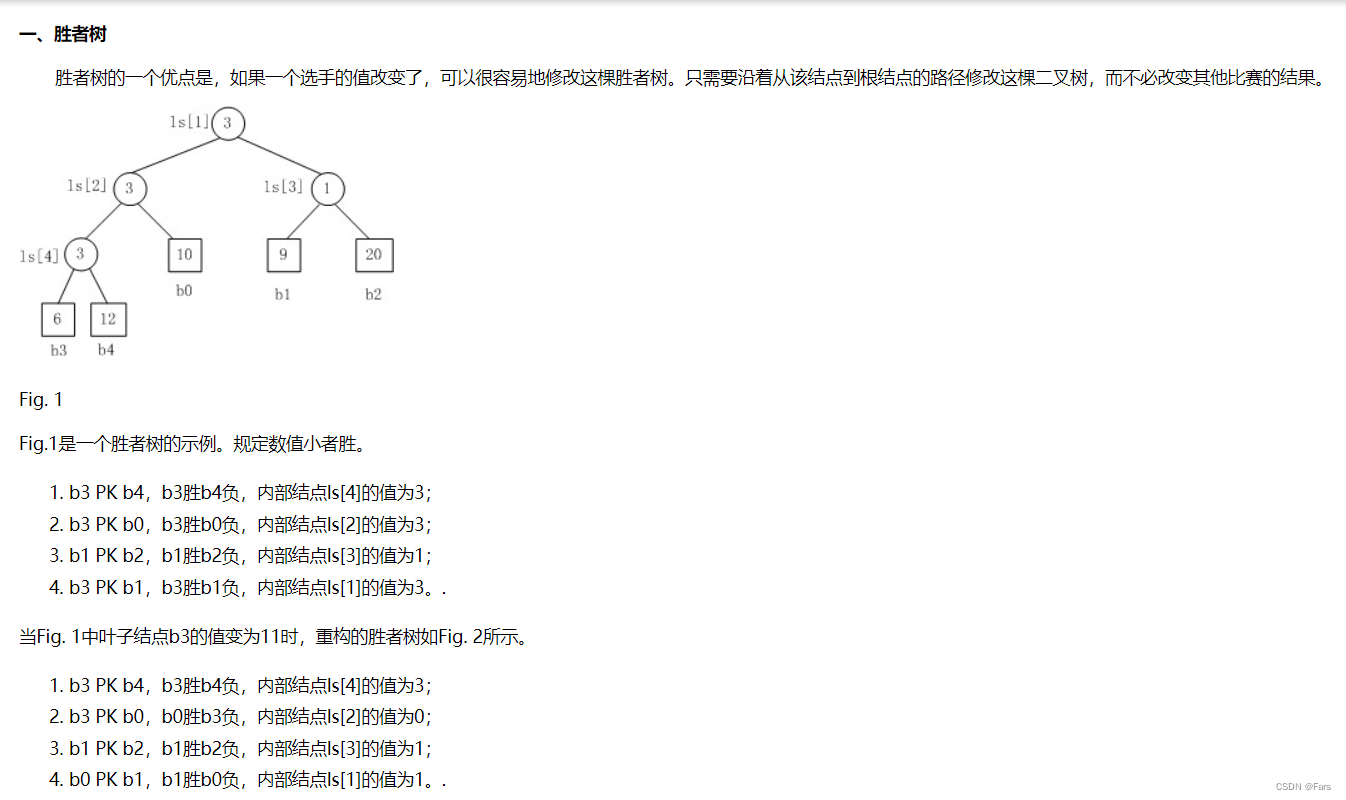
胜者树图

img点击并拖拽以移动编辑

败者树图

img点击并拖拽以移动编辑

img点击并拖拽以移动编辑

img点击并拖拽以移动编辑外排序算法 — WZX’s Blog

败者树的具体实现，java代码

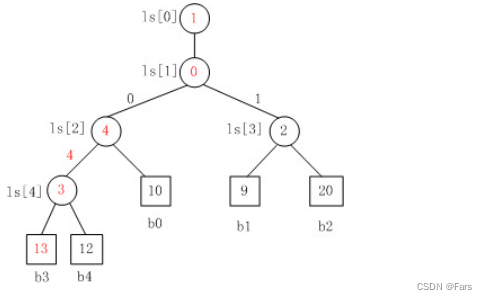
img点击并拖拽以移动编辑

  • 这个按照这个图顺序定义b0,b1~b4的顺序，b0必须从第一个最小叶子结点作为b0，才符合b_parnet = (b_index+b_size)/2

败者树的Java实现

参考败者树的Java实现_solari_bian的博客-CSDN博客

辅助数据结构Chunk与Record

Record就是Chunk流里面具体某个东西，这里以数值a作为排序依据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import java.io.Serializable;
/**
 * 记录类，包含一个整数型属性A和一个字符串型属性B
 */
public class Record implements Serializable {
    private int a;
    private String b;

    public Record(int a, String b) {
        this.a = a;
        this.b = b;
    }

    public int getA() {
        return a;
    }

    public String getB() {
        return b;
    }

    @Override
    public String toString() {
        return "Record{" +
                "a=" + a +
                ", b='" + b + '\'' +
                '}';
    }
    //写compareTo
    public int compareTo(Record o) {
        if (this.a > o.a) {
            return 1;
        } else if (this.a < o.a) {
            return -1;
        } else {
            return 0;
        }
    }
}

点击并拖拽以移动

Chunk就是通过置换-选择排序，得出来的一段已排序好的初始归并段

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
import java.util.ArrayList;
import java.util.List;

/**
 * <h4>szf-lab2</h4>
 * <p></p>
 *
 * @author : Fars
 * @date : 2023-04-27 23:31
 **/
class Chunk{
    public Chunk() {
    }

    public Chunk(int chunkId) {
        this.chunkId = chunkId;
    }

    public Chunk(List<Record> recordList, int chunkId) {
        this.recordList = recordList;
        this.chunkId = chunkId;
    }
    private int chunkId =-1;//未赋值默认为-1
    private List<Record> recordList = new ArrayList<>();
    //实现add
    public void add(Record record){
        recordList.add(record);
    }
    //实现poll
    public Record poll(){
        return recordList.remove(0);
    }

    public List<Record> getRecordList() {
        return recordList;
    }
    //实现getSize
    public int getSize(){
        return recordList.size();
    }
    //实现compareTo
    public int compareTo(Chunk chunk){
        Record record1 = this.recordList.get(0);
        Record record2 = chunk.recordList.get(0);
        return record1.compareTo(record2);
    }
    //实现isEmpty
    public boolean isEmpty(){
        return recordList.isEmpty();
    }

    @Override
    public String toString() {
        return "Chunk{" +
                "chunkId=" + chunkId +
                ", recordList=" + recordList +
                '}';
    }
    public int getChunkId() {
        return chunkId;
    }
}

点击并拖拽以移动

败者树LoserTree，直接运行main即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
import javax.print.attribute.IntegerSyntax;
import java.util.ArrayList;
import java.util.List;
public class LoserTree
{
    private int[] ls = null;// 以顺序存储方式保存所有非叶子结点
    private int size = 0;
    private ArrayList<Chunk> leaves = null;// 叶子节点

    public LoserTree(ArrayList<Chunk> chunks)
    {
        this.leaves = chunks;// 叶子结点
        this.size = chunks.size();// 叶子结点个数 = 块数 = ls个数
        this.ls = new int[size];//ls个数 = 块数 = 叶子结点个数
        for (int i = 0; i < size; ++i)
        {
            ls[i] = -1;
        }
        for (int i = size - 1; i >= 0; --i)
        {
            adjust(i);
        }
    }
    /* 
     * @Description: 从chunks中删除第s块，并调整败者树
     * @param s 
     * @return: void 
     * @Author: Fars
     * @Date: 2023/4/27 23:28
     */
    public void del(int s)
    {
        leaves.remove(s);
        size--;
        ls = new int[size];
        for (int i = 0; i < size; ++i)
        {
            ls[i] = -1;
        }
        for (int i = size - 1; i >= 0; --i)
        {
            adjust(i);
        }
    }

    public void add(Chunk leaf, int s)
    {
        leaves.set(s, leaf);// 调整叶子结点
        adjust(s);// 调整非叶子结点
    }

    public Chunk getLeaf(int i)
    {
        return leaves.get(i);
    }

    public int getWinnerChunkIndex()
    {
        return ls[0];
    }

    public Chunk getWinnerChunk()
    {
        return leaves.get(ls[0]);
    }
//    public void adjust(int leafIndex)
//    {
//        // s指向当前的值最小的叶子结点（胜者）
//        int parent = (leafIndex + size) / 2;// parent是leafIndex的双亲
//
//        while (parent > 0)// 沿从叶子到根的路径比较，直到根结点
//        {
//            if (leafIndex >= 0 && (ls[parent] == -1 || leaves.get(leafIndex).compareTo(leaves.get(ls[parent])) > 0))
//            {
//                // 将树中的当前结点指向其子树中值最小的叶子
//                int tmp = leafIndex;
//                leafIndex = ls[parent];
//                ls[parent] = tmp;
//            }
//    }

    public void adjust(int leafIndex)
    {
        // s指向当前的值最小的叶子结点（胜者）
        int parent = (leafIndex + size) / 2;// parent是leafIndex的双亲

        while (parent > 0)// 沿从叶子到根的路径比较，直到根结点
        {
            int winnerIndex;
            int loserIndex;
            //如果是父节点ls[parent]为-1,代表还没有比赛过，应该要和兄弟比赛
            if(ls[parent] == -1){
                if (leaves.get(leafIndex).compareTo(leaves.get(leafIndex - 1)) < 0){
                    winnerIndex = leafIndex;
                    loserIndex = leafIndex - 1;
                }
                else{
                    winnerIndex = leafIndex - 1;
                    loserIndex = leafIndex;
                }
            }
            //如果s战胜了父亲节点代表的leaf ( leave.get(s) < leaves.get(ls[parent]) )，那么胜者是s
            else if(leaves.get(leafIndex).compareTo(leaves.get(ls[parent])) < 0){
                winnerIndex= leafIndex;
                loserIndex = ls[parent];
            }
            else{
                winnerIndex = ls[parent];
                loserIndex = leafIndex;
            }
            //将败者索引放到父亲节点
            ls[parent] = loserIndex;
            //将胜者继续向上比较
            leafIndex = winnerIndex;
            parent /= 2;
        }
        ls[0] = leafIndex;// 树根指向胜者
    }

    public static void main(String[] args) {
        //给定示例输入数据
        ArrayList<Chunk> chunks = new ArrayList<Chunk>();
        Chunk chunk1 = new Chunk(0);
        chunk1.add(new Record(1,"record_1"));
        chunk1.add(new Record(7,"record_7"));
        chunk1.add(new Record(8,"record_8"));
        Chunk chunk2 = new Chunk(1);
        chunk2.add(new Record(4,"record_4"));
        chunk2.add(new Record(5,"record_5"));
        chunk2.add(new Record(6,"record_6"));
        chunks.add(chunk1);
        chunks.add(chunk2);
        //利用败者树排序
        LoserTree loserTree = new LoserTree(chunks);
        //输出排序结果
        System.out.println("排序结果：");
        while(true) {
            System.out.println("当前winner代表的chunkIndex = " + loserTree.getWinnerChunkIndex());
            System.out.println("该chunk = " + loserTree.getWinnerChunk().toString());
            System.out.println("该chunk的块首元素 = " + loserTree.getWinnerChunk().poll());
            int chunkIndex = loserTree.getWinnerChunkIndex();
            Chunk winnerChunk = loserTree.getWinnerChunk();
            //如果该chunk为空，则去除该chunk
            if (loserTree.getWinnerChunk().isEmpty())
            {
                loserTree.del(chunkIndex);
                System.out.println("删除chunk，其Id:" + winnerChunk.getChunkId());
                if(chunks.size() == 0)
                    break;
            }

            else//否则调整败者树
                loserTree.adjust(chunkIndex);
        }
    }
}

点击并拖拽以移动

整个外部排序的模拟实现代码

有些许bug，应该无伤大雅

代码太多，就不放上来了，请看github

外部排序完整代码 https://github.com/944613709/external-sorting-of-k-way-multi-way-merge-sorting

算法
#外部排序
外部排序&&败者树&&k路归并排序
http://yoursite.com/2023/04/28/外部排序&&败者树&&k路归并排序/
作者
Fars
发布于
2023年4月28日
许可协议